Spring Offerings.
EN.520.653: Dynamics & Control of Modern Power Systems
Advanced Graduate Course
Course Description
This course covers the fundamental theory of dynamic analysis and control of modern power systems. Topics include mathematical modeling of large-scale power systems, linear and nonlinear system theory (for example, Lyapunov stability, bifurcation), small- and large-disturbance analysis, and voltage stability and control. Furthermore, various emerging challenges and opportunities in future low-inertia power systems are discussed. Selective topics include inverter-based resources (IBRs), renewable generation, system resilience, advanced control strategies, and smart grid technologies. Some unique perspectives are provided, such as limit-induced bifurcation, trajectory sensitivity, and hybrid dynamics.
- This course entails a relatively heavy emphasis on mathematical analysis and proof. Sufficient mathematical maturity is expected from the students.
- There will be in-class group discussions on research papers. Students will complete an individual term project that focuses on a research question related to the class topics.
Prerequisites
- Required: Calculus I, II & III, Control Systems (EN.520.353 or the equivalent). Solid knowledge on electric circuits, complex variables, ordinary differential equations, and linear algebra. Familiar with MATLAB programming.
- Preferred: Energy Systems (EN.560.649 or the equivalent), Introduction to Linear Systems Theory (EN.530.616 or the equivalent).
Principle Course Modules
- Module 1: Introduction to power system dynamics and control
- Module 2: Power flow analysis
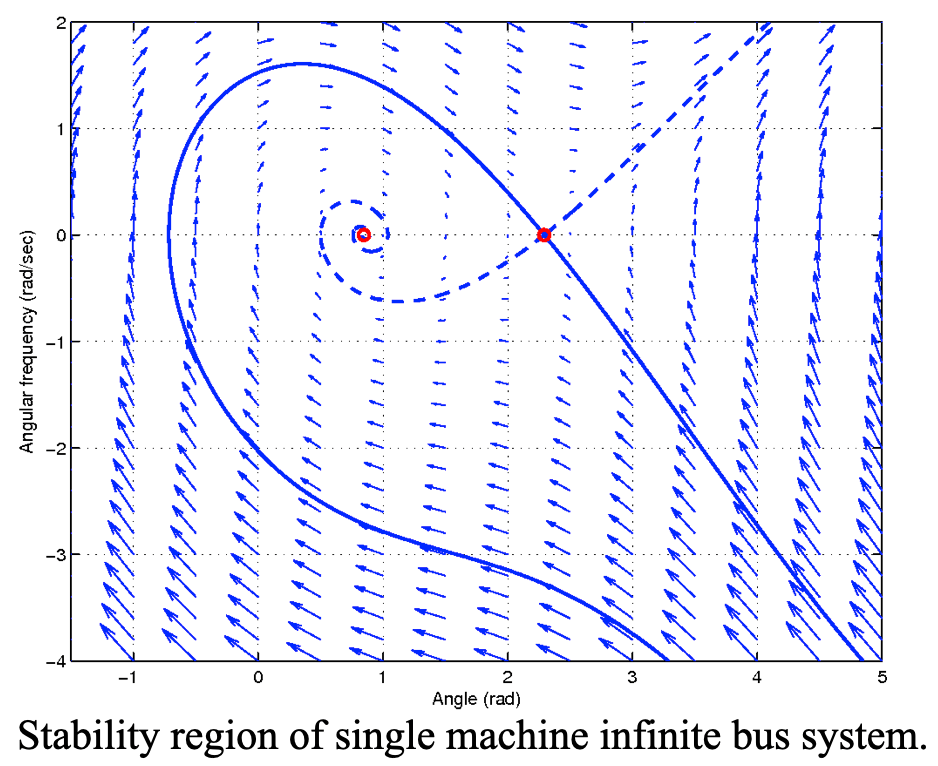
- Module 3: Stability concepts
-
Module 4: Small-disturbance (linear) analysis
-
Module 5: Large-disturbance analysis: Analytical
-
Module 6: Large-disturbance analysis: Numerical
-
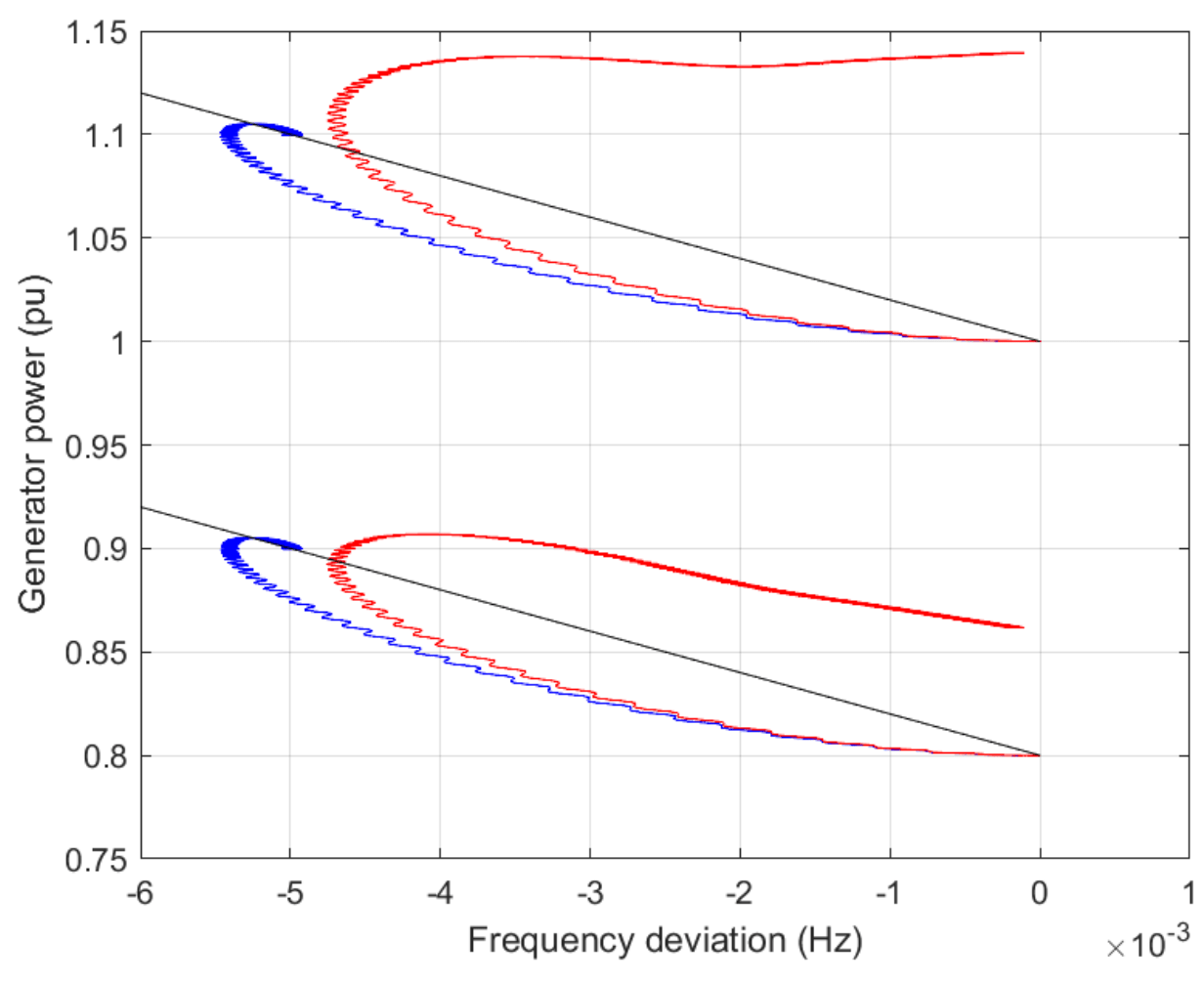
Module 7: Modeling and control: Inverter-based resource
-
Module 8: Modeling and control: Synchronous machine
-
Module 9: Emerging topics (paper discussion)
Course Objectives
Some specific outcomes for this course include:
- Students will grasp the methodologies of modeling, analysis and control of dynamical systems, including both linear and nonlinear systems.
- Students will gain a thorough understanding of power system engineering.
- Students will have a good understanding of the challenges and opportunities that arise during the energy transition to future low-inertia (renewable) power systems.
- Students will be able to evaluate research papers and propose research questions.
- Students will improve their abilities to engage in collaborative work, discussion, and presentation.
Fall offerings.
EN.520.454/654: Control Systems Design
Undergrad and Graduate Course
Course Description
This course covers classical and modern control systems design methods. Topics include formulation of design specifications, pole placement and eigenvalue placement, frequency-domain design, design of compensators, state and observer-based feedback, linear quadratic control, discrete-time control, and Lyapunov-based analysis and design.
- This course entails a relatively heavy emphasis on mathematical analysis and proof. Sufficient mathematical maturity is expected from the students.
- Students will complete an individual term project. Computers are used extensively for design.
Prerequisites
- Required: EN.520.353: Control Systems (or equivalent). AS.110.201: Linear Algebra (or equivalent). Proficient with MATLAB & Simulink.
- Preferred: Introduction to Linear Systems Theory (EN.530.616 or the equivalent).
Principle Course Modules
- Module 1: Introduction (Open-loop vs. closed–loop control; Linear vs. nonlinear systems; External vs. internal stability)
- Module 2: Performance specification (Steady–state and transient; Internal model principle)
- Module 3: Pole placement (Sylvester’s theorem)
-
Module 4: Eigenvalue placement (Controllable canonical form; Ackermann’s formula)
-
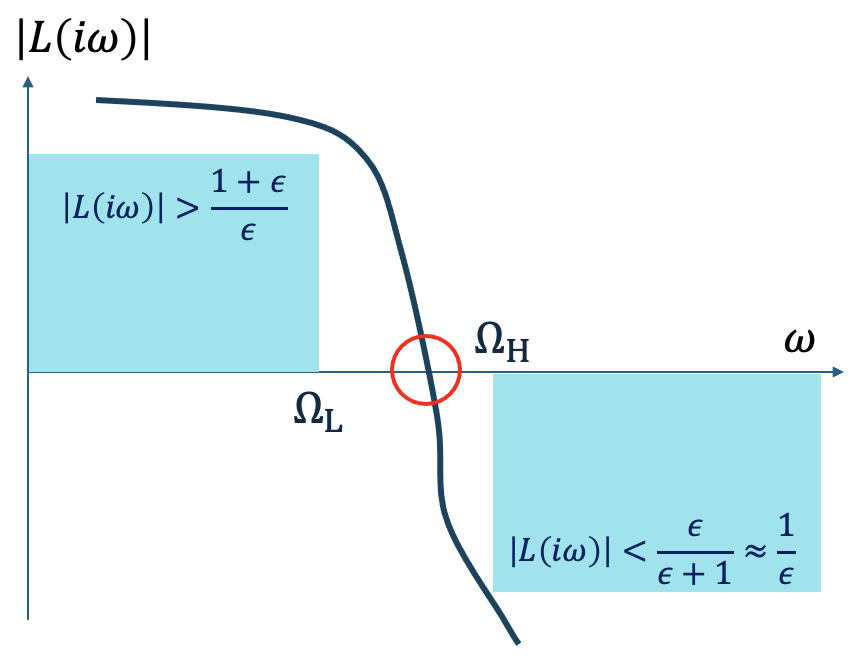
Module 5: Frequency domain analysis & design (Bode plot and Nyquist plot)
-
Module 6: Loop shaping control (Tracking and robustness; Fundamental tradeoffs)
-
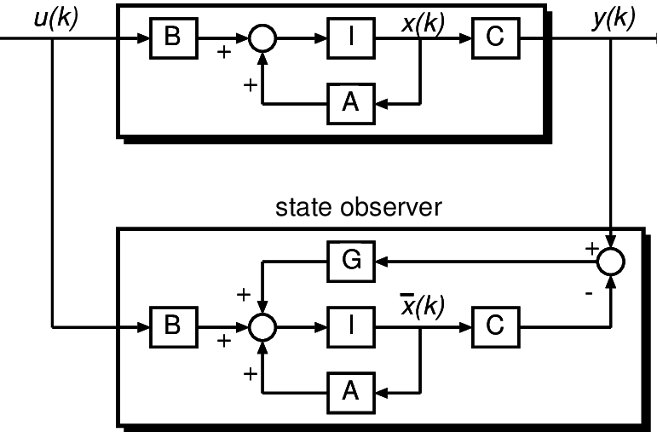
Module 7: Observer design (Observable canonical form; Full-order and reduced-order)
-
Module 8: Linear quadratic control; Linear quadratic estimator (Algebraic Riccati equation)
-
Module 9: Discrete-time modeling & control
- Module 10: Term design project (5 weeks)
Course Objectives
Some specific outcomes for this course include:
- Students will grasp methods for control systems design and apply them to a project.
- Students will have a good understanding of the principles of control systems.
- Students will be able to use computer to analyze systems and program controllers.
- Students will improve their abilities to engage in collaborative work, discussion, and presentation.