Research Projects
- Dynamics, Control, and Stability of Large-Scale Inverter-Based Power Systems
- Analysis and Control of Nonlinear and Hybrid Dynamical Systems
- Optimization of Integrated Energy Systems and Electrified Transportation Systems
- Data-Driven Decision-Making in Networked Dynamical Systems
- Differential Geometry Methods for Power System Analysis
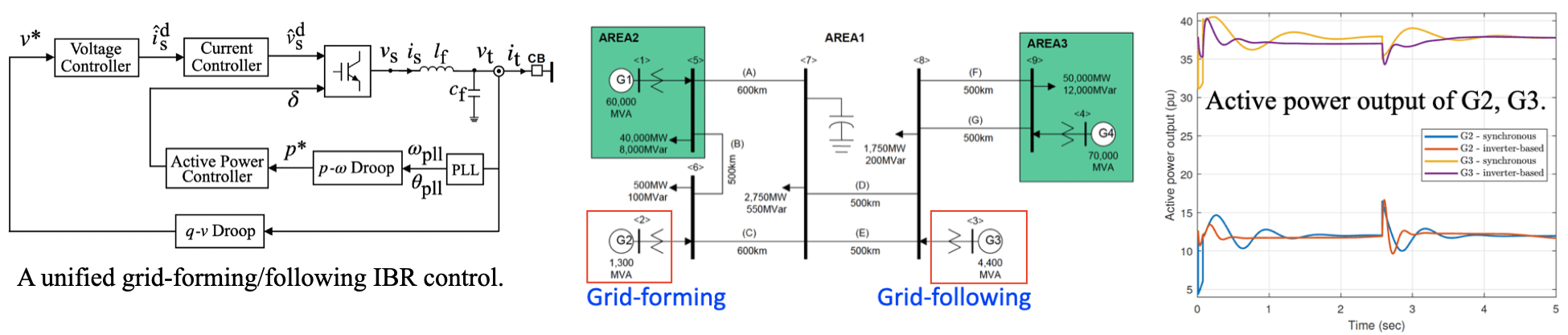
Dynamics, Control, and Stability of Large-Scale Inverter-Based Power Systems
Power systems are expected to host hundreds of millions of distributed inverter-based resources (IBRs) in the near future. IBR-dominated power grids face significant fluctuations in operating conditions, a lack of transparency in control implementations, and unprecedented complexity in dynamic behavior. Left unaddressed, naïve integration of IBRs will lead to reduced reliability and increased conservativeness in operations. This project aims to develop a modeling, analysis, and control design framework to ensure the stability of large-scale inverter-based power systems.
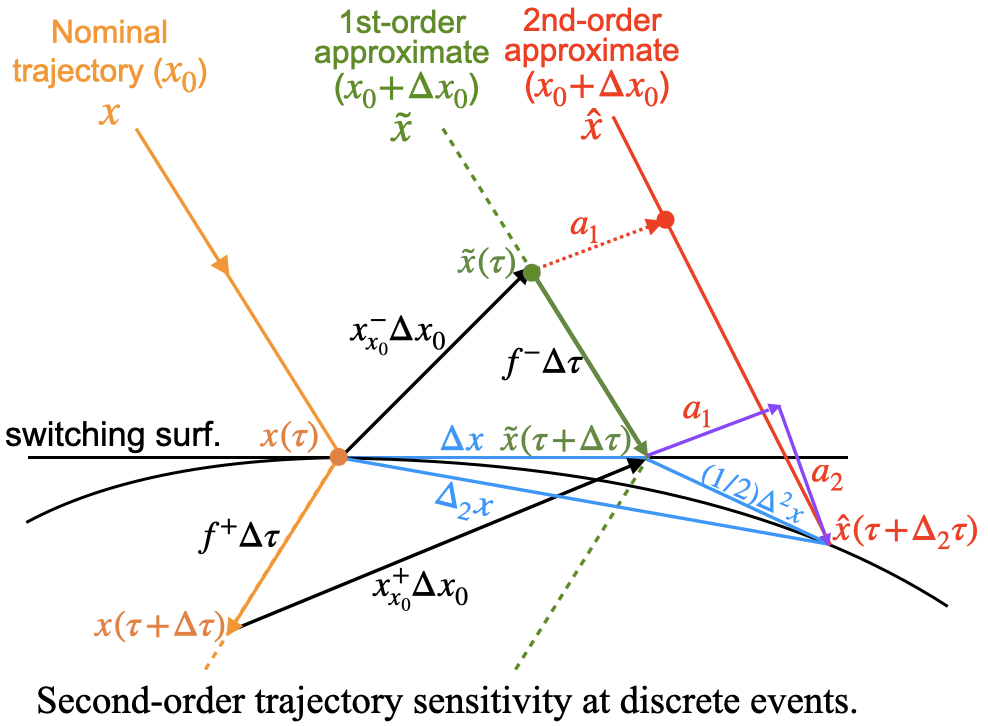
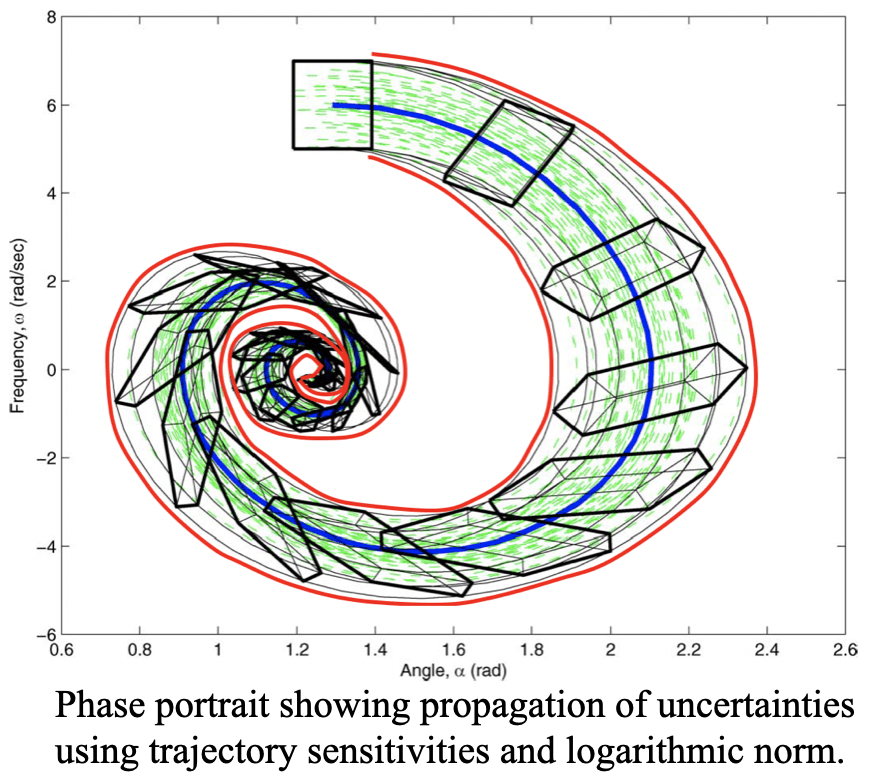
Analysis and Control of Nonlinear and Hybrid Dynamical Systems
Many critical infrastructure systems that support modern societies, such as energy systems, transportation systems, and information systems, can be modeled as large-scale networked dynamical systems. However, nonlinearities and hybrid dynamics, heterogeneity, model uncertainty, and large scale, when combined render existing analysis and control tools over conservative or infeasible. This project adopts a systematic approach rooted in system theory to address the analysis and control of nonlinear and hybrid dynamical systems. The aim of this project is to develop rigorous theory and scalable algorithms to ensure the stability and dynamic performance of such systems.
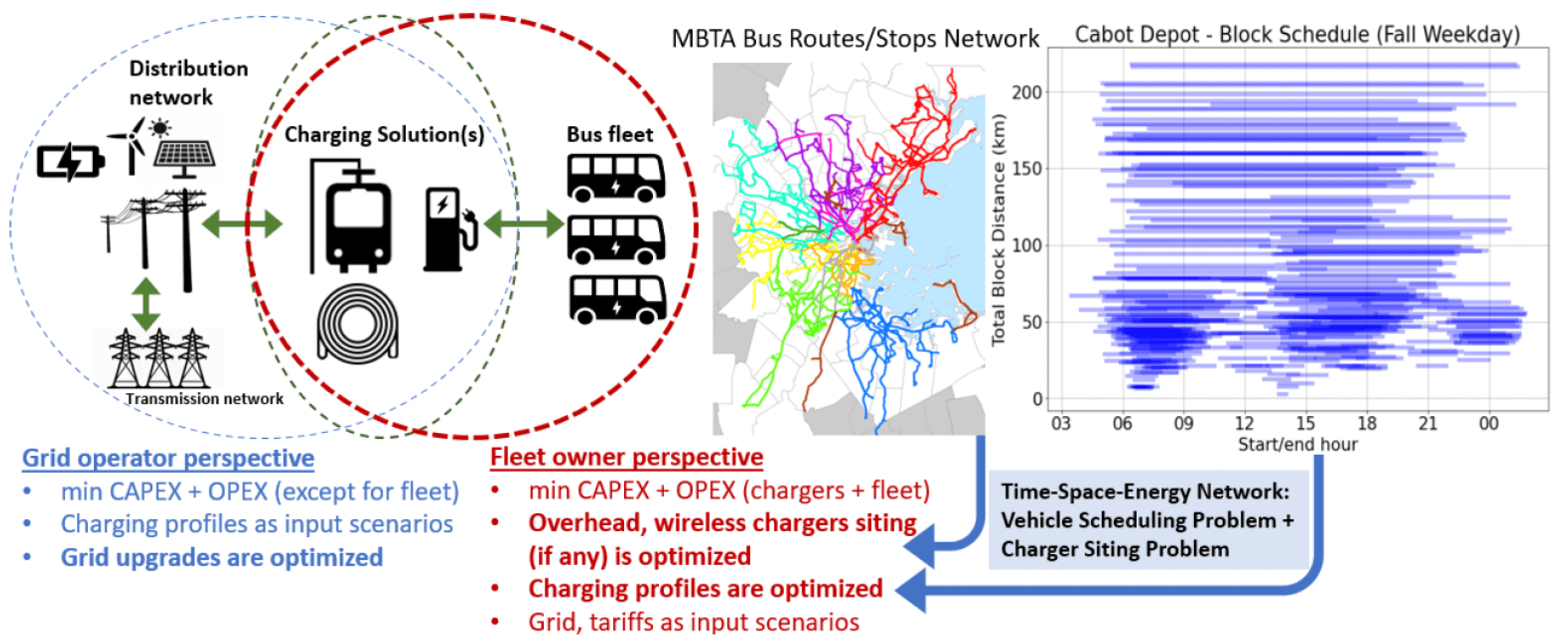
Optimization of Integrated Energy Systems and Electrified Transportation Systems
Next-generation energy systems will integrate multiple energy carriers, including electricity, natural gas, and hydrogen, together with their energy transformation process and storage. Moreover, electric vehicles lead to a tighter integration between transportation and energy systems. This project aims to develop computationally efficient large-scale optimization tools and algorithms to achieve optimal design and operation of such integrated multi-energy systems, with a focus on managing uncertainties. Real geospatial data for transportation schedules, renewable generation, load, and meteorological information are adopted, to provide valuable insights into decarbonization across sectors.
Data-Driven Decision-Making in Networked Dynamical Systems
The power industry is facing an imperative need to address the interoperability problem between all resources to prevent instability under a wide range of system conditions. However, real barriers exist due to the fact that system operators do not have detailed models from inverter manufacturers for proprietary reasons and it is also challenging for the manufacturers to test and validate the inverter against the large-scale power network. To inform the regulators, system operators, and inverter manufacturers and owners, in this project we develop decentralized and robust methods to certify the stability of the overall system using local data observations.
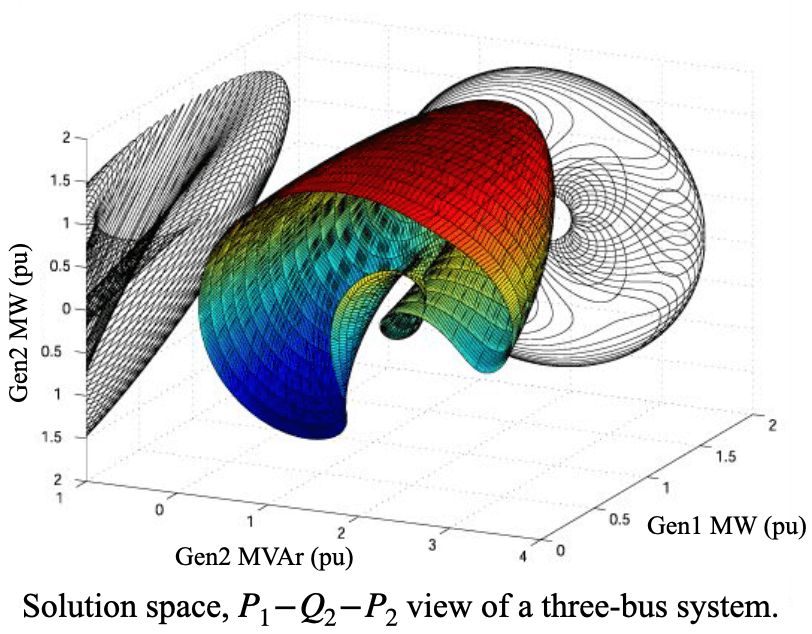
Differential Geometry Methods for Power System Analysis
The power flow equation is a set of nonlinear equations whose solution space is extremely complex. Being able to characterize the structure of the solution manifold is important to evaluate the robustness of operating points and their proximity to voltage collapse. However, existing methods such as continuation power flow and numerical optimization struggle to meet the challenges in future renewable-sourced power systems that feature significant variations in operating points (that are larger in magnitude, faster in timescale, and in higher-dimensional space). In this project, we propose completely novel methods rooted in differential geometry to replicate the global geometry of the solution boundary merely from local measurements and efficient computations.